🇪🇸 Reservoir sampling
Cuando se trata de elegir un elemento aleatorio con igual probabilidad de entre los elementos de un array lo primero que hacemos es buscar el "método random int" en el lenguaje de programación en cuestión y generar un entero entre 0 y el número de elementos - 1 (suponiendo que el primer índice del array es 0). Utilizamos ese número como índice y devolvemos el elemento que se encuentra en esa posición. El generador de enteros aleatorios debe seguir una distribución uniforme, es decir, todos los números enteros en el rango indicado tienen la misma posibilidad de ser elegidos.
Un ejemplo de código en Python que selecciona un número aleatorio de una lista sería:
import random
my_list = [1, 2, 3, 4]
idx = random.randint(0, len(my_list) - 1)
my_list[idx] # Un elemento cualquiera de la lista.
En función del lenguaje de programación seleccionado la sintaxis puede variar,
pero la lógica es la misma.
Algo digno de mención de esta implementación de randint es que el segundo
parámetro (el número máximo a generar) está incluido entre los números
generados, por lo que tenemos que restarle 1.
Nota: en Python podríamos usar directamente random.choice(my_list) para
obtener un elemento aleatorio sin tener que generar el índice nosotros, pero
es generado internamente.
¿Cómo haríamos eso mismo sobre una lista de la que no sabemos el número total de elementos? Es posible que la lista sea tan grande que no quepa en memoria, o simplemente, en lugar de una lista, tenemos un stream continuo de datos y queremos devolver (cuando el stream finalize) un elemento siguiendo una distribución uniforme.
Vamos a soluciona este problema paso a paso.
Continuaré usando Python para mostrar un ejemplo de implementación.
Como siempre, en primer lugar los imports.
Usaré NumPy por costumbre, pero se podría hacer perfectamente usando listas
normales de Python, como se mostró en el primer ejemplo.
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
# Número de elementos de la lista generada.
N_ELEMENTS = 10
# Semilla aleatoria para reproducir experimentos.
SEED = 124
np.random.seed(SEED)
Después de los imports y de fijar una semilla aleatoria para poder reproducir
experimentos, generaremos una lista aleatoria.
La lista contine números enteros en el rango [-n_elements, -1].
Decidí poner los números negativos para diferenciar entre los índices del array
y los valores del array.
El desordenar los números es para darle un aspecto más caótico :)
def get_random_list(n_elements):
# Generamos lista ordenada desde -n_elements hasta -1.
random_list = np.arange(0, n_elements) - n_elements
# Desordenamos la lista.
random_list = np.random.permutation(random_list)
return random_list
random_list = get_random_list(N_ELEMENTS)
random_list
Si utilizas la misma semilla aleatoria que yo, la lista aleatoria random_list
debe contener:
array([ -4, -2, -7, -5, -6, -10, -1, -8, -3, -9]).
Aunque se trate de un array de NumPy, el objeto random_list se puede utilizar
en la mayoría de los casos como una lista de Python.
Por ejemplo, podemos ejecutar la siguiente línea para obtener el tamaño del
array:
Sin embargo, si convertimos la lista en un iterador no podríamos hacer eso.
Ejecutar len(iter(random_list)) daría error.
Utilizaremos iteradores para simular ese stream de longitud indeterminada del
que hablamos antes.
Una solución honrada a este problema sería pensar de la siguiente forma: Muy bien, no tenemos la longitud de la lista pero podemos recorrer el iterador hasta que nos quedemos sin elementos. De esta forma sabríamos el número total de elementos con los que contamos y podríamos utilizar el método "clásico" que ya conocemos que nos permite seleccionar elementos random de una lista siguiendo una distribución uniforme.
Pues sí, podría hacerse eso. ¿El problema? Que necesitaríamos ir guardando todos los elementos que vamos iterando para poder elegir uno. Esto viola una de las condiciones iniciales del enunciado del problema: no queremos mantener toda la lista en memoria.
De todas formas, vamos a implementar este método para comprobar que funciona.
def sample_list(random_iter):
# Convertimos el iterador en una lista.
random_list = [i for i in random_iter]
# Obtenemos un elemento aleatorio como hicimos anteriormente.
length = len(random_list)
idx = np.random.randint(0, length - 1)
return random_list[idx]
sample_list(iter(random_list))
Esto parece funcionar y devuelve un elemento aleatorio de la lista.
Con mi semilla aleatoria el resultado es -10.
De todas formas vamos a repetir este proceso muchas veces y pintar en un histograma la frecuencia con la que se elige cada elemento.
def test_sample_method(method, random_list, n_times):
samples = []
for i in range(n_times):
samples.append(method(iter(random_list)))
plt.hist(samples)
test_sample_method(sample_list, random_list, 40)
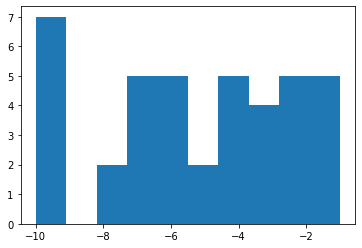
El resultado es bastante interesante. ¿Casualmente no se ha elegido el número -9 o hay un fallo en nuestra función? Ejecutemos unos cuantos experimentos más para asegurarnos que no ha sido casualidad. En lugar de 40 ejecutemos 10000.
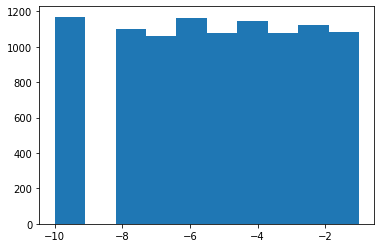
Parece que tenemos un fallo en nuestro selector de samples. ¿Lo ves?
Al contrario de lo que hacíamos en el primer ejemplo de código con el que
se iniciaba el post, aquí no estamos generando el número aleatorio usando
Python, sino que estamos usando la función de NumPy np.random.randint.
Esta función no incluye el último elemento entre los devueltos, por lo que no
es necesario restarle 1 al segundo parámetro.
El elemento -9 nunca era devuelto puesto que es el último de la lista.
Corregimos el error y volvemos a pintar el histograma.
def sample_list(random_iter):
random_list = [i for i in random_iter]
length = len(random_list)
# Ya no ponemos lenght - 1!!
idx = np.random.randint(0, length)
return random_list[idx]
test_sample_method(sample_list, random_list, 10000)
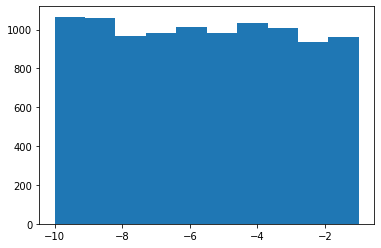
Ahora sí observamos que cada unon de los números ha sido elegido un número similar de veces.
Pues bien, ya tenemos el framework montado para escribir una función
distinta a sample_list que resuelva el problema de una forma más eficiente
(sin tener que mantener en memoria toda la lista).
¿Alguna otra idea de cómo resolverlo?
Podríamos leer primero el stream para averiguar el número de elementos, generar un número aleatorio en el rango de la lista y, posteriormente, volver a leer el stream desde el principio y seleccionar el elemento que se corresponde con el índice seleccionado. Esta otra opción tiene un punto débil muy claro: debemos de leer el stream 2 veces. Directamente nos saltaremos esta implementación e iremos con la forma más eficiente: un algoritmo que nos permite hacer esa selección leyendo una única vez el stream y sin almacenar toda la lista en memoria.
Reservoir sampling
Todo lo anterior comentado no es más que una introducción larga para llegar a la descripción del algoritmo reservoir sampling. El funcionamiento de este algoritmo se basa en seleccionar aleatoriamente elementos provisionales hasta que termina el stream. Cuando finaliza el stream, el último elemento provisional seleccionado es devuelto, de forma que la probablidad de seleccionar un elemento del stream es exáctamente la misma para todos los elementos. Guardando únicamente un solo elemento en memoria la complejidad espacial de este algoritmo es \(\(\mathcal{O}(1)\)\) y, puesto que solo se leen los elementos una vez, la complejidad temporal es \(\(\mathcal{O}(n)\)\) siendo \(n\) el número de elementos del stream.
Formalizemos el problema usando matemáticas. Queremos que la probabilidad de elegir un elemento \(\(x_i\)\) de la lista \(\(\mathbf{x} = {x_1, x_2, \cdots, x_n}\)\) sea \(\(P(x_i) = \dfrac{1}{n}\)\) para todo valor de \(\(1 \leq i \leq n\)\).
Supón que comienza el stream y recibes un elemento. Si dejamos pasar ese elemento y el stream finaliza sin darte ningún elemento más, tendríamos un problema puesto que nuestro algoritmo no devolvería ningún elemento aleatorio de la lista. El primer elemento hay que cogerlo sí o sí. Con cogerlo me refiero a guardarlo temporalmente en memoria. Si el stream termina ahí, tendríamos que devolver ese elemento sin más. Esto tiene sentido puesto que cuando tenemos un solo elemento en la lista la probabilidad de cogerlo es 1: $$ P_1(x_1) = \dfrac{1}{n} = \dfrac{1}{1} = 1 $$. Con \(\(P_1\)\) indico que hemos leído un solo elemento del stream.
Si el stream no termina, hay que seguir leyendo elementos y sustituir
aleatoriamente el antiguo elemento por uno de los nuevos.
Cuando leemos un segundo elemento deberíamos tener:
$$
P_2(x_2) = \dfrac{1}{n} = \dfrac{1}{2} = 0.5
$$.
Es decir, la mitad de las veces sustituiríamos el elemento provisional (el
primer elemento) por el segundo.
Para realizar esto en Python podemos evaluar la condición
np.random.randint(0, 2) == 0.
La función randint nos devolverá o un 0 o un 1 de manera uniforme, por lo que
la mitad de las veces será 0.
Si se cumple la condición, podremos sustituir el elemento provisional por el
nuevo.
\(\(P_2(x_2) = 0.5\)\), tal y como debería de ser. Pero ahora que hemos añadido un elemento nuevo ¿cuál es la probabilidad de acabar eligiendo el primer elemento? Es decir, ¿cuánto vale \(\(P_2(x_1)\)\)? ¿Sigue siendo \(\(P_2(x_1) = P_1(x_1) = 1\)\)? Ovbiamente ya no es 1 puesto que la mitad de las veces será sustituido por el segundo elemento. La nueva probabilidad de elegir el primer elemento es la probabilidad de elegir el elemento en el paso anterior (\(\(P_1(x_1)\)\)) por la probabilidad de no elegir el segundo elemento (\(\(1 - P_2(x_2)\)\)). Traduciendo a una expresión matemática tenemos que: $$ P_2(x_1) = P_1(x_1) \cdot (1 - P_2(x_2)) = 1 \cdot (1 - 0.5) = 0.5 $$. La posible sustitución de \(\(x_1\)\) cuando se lee el segundo elemento cambia la probabilidad de elegir \(\(x_1\)\), y dicha probabilidad coincide con una distribución uniforme.
Podría seguir derivando para un tercer elemento, pero directamente voy a escribir la expresión general.
para todo valor de \(\(i < n\)\).
Ahora, partiendo de la expresión general obtengamos la expresión para 3 elementos.
Como se observa, \(\(P_3(x_1) = P_3(x_2) = P_3(x_3) = \dfrac{1}{3}\)\), por lo que cumple con los requisitos.
Implementación
La implementación es muy sencilla, la puedes encontrar justo debajo.
def sample_reservoir(random_iter):
# Cogemos el primer elemento como elemento provisional.
sample = next(random_iter)
for i, n in enumerate(random_iter):
# Cambiamos el sample cada vez que leemos un nuevo elemento con
# probabilidad 1 / n_elementos_leidos.
if np.random.randint(0, i + 1) == 0:
sample = n
# Devolvemos el último sample seleccionado.
return sample
sample_reservoir(iter(random_list))
Con mi semilla aleatoria me proporciona un -5.
Pintemos el histograma después de haber seleccionado 10000 elementos.
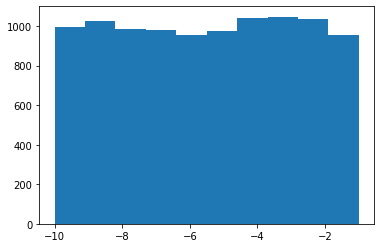
Efectivamente, con esta nueva función también obtenemos un histograma propio de una distribución uniforme. ¡Misión cumplida!
Puedes encontrar un notebook de Python con el código en el repositorio. Recuerda que para obtener exactamente los mismos resultados debes de ejecutar el notebook de principio a fin, puesto que la semilla aleatoria se configura al principio. Si ejecutas una celda dos veces hará que el resultado de las siguientes no sea exactamente el mismo que el mío.