🇪🇸 Euler Phi/Totient function
Esta semana me topé con este problema en una competición de CodeForces. Es bastante obvio que no se puede resolver con fuerza bruta para valores grandes. ¿Cómo se resuelve entonces? Primero analicemos el problema y luego os presentaré a la función matemática aliada que nos ayudará en la batalla contra este enunciado.
El enunciado es el siguiente. Tenemos dos números enteros \(a\) y \(m\) tal que \(1 \le a < m \le 10^{10}\) y el problema nos pide que contemos cuantos valores puede tomar el entero \(x\) tal que \(0 \le x < m\) y se cumpla \(\gcd(a, m) = \gcd(a + x, m)\). \(\gcd\) representa el máximo común divisor (greatest common divisor en inglés).
Greatest common divisor
Lo primero es tener claro el significado de máximo común divisor. El máximo común divisor de dos números cualesquiera es la intersección de los factores primos que forman dichos números. Esta imagen de Wikipedia debería dejar más clara la definición:
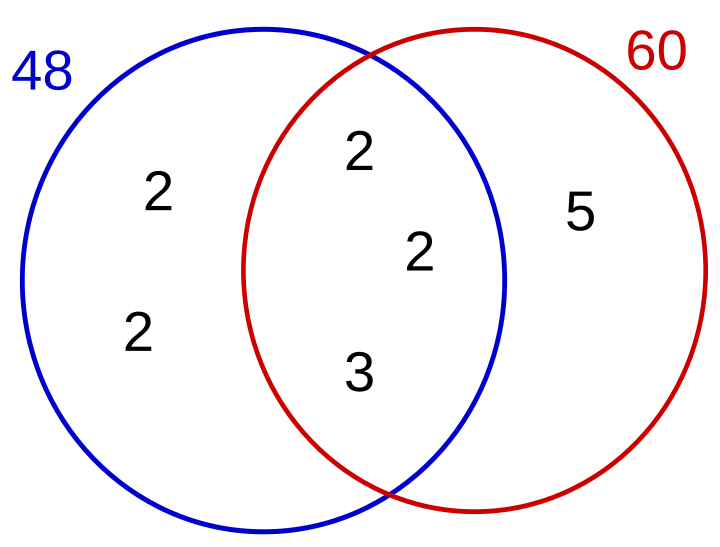
El máximo común múltiplo se resuelve eficientemente usando un algoritmo conocido desde tiempos de la antigua Grecia. Se trata del algoritmo de Euclides.
Desarrollo del problema
Una vez entendidos todos los elementos que aparecen en el enunciado del problema podemos proceder con su resolución.
Definamos \(y = a + x\). ¿Qué podemos decir de los valores de \(y\) que cumplen el requerimiento del enunciado? Sabemos que \(y \in [a, a + m)\) por la propia definición de \(x\) dada en el enunciado. ¿Qué más sabemos? Sabemos que entre los factores primos que componen \(y\) deben encontrarse aquellos que componen \(\gcd(a, m)\), y pueden contener otros factores distintos de aquellos que componen \(\frac{m}{\gcd(a, m)}\) (es decir, los factores que componen \(m\) excepto aquellos que forman parte del \(\gcd(a, m)\)). Utilicemos los números \(a=48\) y \(m=60\) del ejemplo de la anterior imagen para aclarar esto último que he dicho. \(\gcd(48, 60) = 2 \cdot 2 \cdot 3 = 12\). \(y\) debe tener 2, 2, y 3 entre sus factores pero no el 5. Si no tuviera ni 2, 2 o 3 entre sus factores, o si tuviera el 5, \(\gcd(y, 60)\) sería distinto de 12. Dicho de otra forma, \(y\) debe de ser un múltiplo de 12 que no contenga el 5 entre sus factores.
Vamos a definir \(y = 12 \cdot k\), ¿cuántos valores de \(k\) no contienen el número 5 entre sus factores? Dicho de otra forma, ¿cuántos números primos relativos a 5 hay? Realmente hay infinitos, pero ¿cuántos hay en el rango \(y \in [a, a + m) = [48, 48+60) = [48, 108)\)? Los valores que puede tomar \(k\) son 4, 5, 6, 7 y 8 para que \(y\) esté en el rango indicado. De todos esos, obviamente el 5 no es primo relativo de 5. Por lo que hay cuatro valores válidos de \(k\).
Valores válidos de \(k\)
\(\color{red}k = 3 \to y = 12 \cdot 3 = 36 \notin [48, 108)\)
\(\color{green}k = 4 \to y = 12 \cdot 4 = 48 \in [48, 108)\)
\(\color{red}k = 5 \to y = 12 \cdot 5 = 60 \in [48, 108)\), aunque está en el intervalo no es primo relativo de 5.
\(\color{green}k = 6 \to y = 12 \cdot 6 = 72 \in [48, 108)\)
\(\color{green}k = 7 \to y = 12 \cdot 7 = 84 \in [48, 108)\)
\(\color{green}k = 8 \to y = 12 \cdot 8 = 96 \in [48, 108)\)
\(\color{red}k = 9 \to y = 12 \cdot 9 = 108 \notin [48, 108)\)
¿Cómo podemos simplificar ese cálculo? Para ello hay que darse cuenta de una cosa. Para todo valor de \(y > m, \gcd(y, m) = \gcd(y - m, m)\). Si esto no te convence haz una pausa y convéncete a ti mismo de que esto es así. Busca recursos sobre el máximo común divisor para entenderlo mejor. Además, como \(0 \le x < m\), sabemos que hay \(m\) valores distintos de \(x\). Esto básicamente transforma nuestra pregunta a: ¿cuántos valores de \(k\) menores de 5 son coprimos de 5?
Euler Phi function o Euler Totient function
La respuesta directa a esta pregunta la da la función \(\varphi(n)\) de Euler, también conocida como la función indicatriz de Euler (Totient function en inglés). Esta función devuelve la cantidad de números menores de \(n\) que son primos relativos de \(n\). Justo lo que necesitamos.
Puesto que esta función nos da lo que necesitamos, lo que debemos programar es:
Vamos a ir desgranando el comportamiento de esta función. Empezando con una definición formal, que no viene siendo más que la forma matemática de escribir lo comentado en el párrafo anterior.
\(\varphi(m)\) es el número de elementos (denotado por \(|\cdot|\)) del conjunto (\(\{\cdot\}\)) formado por los números naturales (\(\mathbb{N}\), no incluye el 0) que son menores de \(m\) y que son primos relativos o coprimos de \(m\) (dicho de otra forma, \(\gcd(m, n) = 1\)).
Empecemos con algún ejemplo. Supongamos que queremos obtener todos los números menores de 11 y coprimos a 11. Pues bien, es fácil darse cuenta de que 11 es un número primo, por lo que hay 10 números naturales menores que 11 que no comparten ningún factor primo con él:
Siendo \(p\) un número primo, la fórmula general es:
¿Qué pasa con \(\varphi(8)\)?
8 no es primo, pero puede descomponerse fácilmente en \(2^3\). 8 es en realidad la potencia de un primo \(p = 2\). En lugar de pintarlo como una lista vamos a distribuirlo como una matriz con \(p\) columnas:
Se observa que la última columna contiene todos los múltiplos de \(p\), lo cuál es bastante obvio porque la última columna es la columna \(p\). Para extraer la fórmula general de \(\varphi(p^n)\) quizás sea útil pintar otro ejemplo. Pintemos \(\varphi(3^2)\):
Puedes pintar algunos casos más si lo deseas, pero yo paso directamente a mostrarte la expresión general. La forma de calcularlo es tomando el total de números y restándole la cantidad de números que hay en la última columna:
¿Problemas para entender la fórmula anterior?
Sabemos que la matriz que hemos definido tiene \(p\) columnas. También sabemos que hay \(p^n\) elementos en la matriz. ¿Cuántos elementos hay en cada columna? Llamemos \(x\) al número de elementos en cada columna. Podemos decir que \(p\) columnas multiplicado por \(x\) elementos que hay en cada columna debe darnos el total de elementos, por lo que \(px = p^n\). De ahí obtenemos que \(x = p^{n - 1}\).
Seguimos. ¿Cuánto vale \(\varphi(15)\)? 15 no es primo ni es la potencia de un primo, así que la fórmula anteriormente expuesta no sirve. \(15 = 3 \cdot 5\), por lo que cualquier número menor de 15 que esté formado por el factor primo 3 o el factor primo 5 no es coprimo de 15 y no debemos de contarlo.
De nuevo, pintemos en forma de matriz los números:
Esta vez es más difícil de verlo, pero tenemos que \(\varphi(15) = \varphi(3) \varphi(5) = 2 \cdot 4 = 8\). Si calculamos el resto (operación módulo) de cada uno de los valores al dividirlos entre 3, todos los números de una columna dan el mismo resto: la primera columna resto 1, la segunda columna resto 2 y la última columna resto 0. Si calculamos el resto para el 5 obtenemos que en cada columna los restos son todos distintos unos a otros, es decir, que los restos van de 0 a 4. Por ejemplo, en la primera columna de arriba a abajo los restos son: 1, 4, 2, 0 y 3. Todos los números son distintos, y solo el elemento que da de resto 0 es múltiplo de 5.
Dicho de otra forma, de esas 3 columnas, en una de ellas todos los números son múltiplos de 3. Las otras dos son números coprimos a 3. De esas dos columnas restantes, solo 4 de los 5 valores son primos relativos de 5, por lo que tenemos \(2 \cdot 4 = 8\) coprimos de 15.
Esto se puede probar más rigurosamente pero no lo haré en este artículo. En las referencias podrás encontrar otros recursos que profundizan más en el tema.
De forma más general, para cualquier número \(n = p_1^{e_1} p_2^{e_2} \ldots p_t^{e_t}\), siendo \(p_i^{e^i}\) el \(i\) primo que compone \(n\) y \({e^i}\) el número de veces que aparece dicho primo en la descomposición, se puede escribir la siguiente expresión general:
Implementación
La implementación no tiene mayor historia, es implementar una factorización y posteriormente una multiplicación de los primos (ignorando el exponente de dichos primos).
La implementación de \(\gcd(a, b)\) que usamos es la que está incluida en el
módulo estándar de Python math.
def prime_factors(n):
"""Return a list of the prime factors that compose n. """
# Factorization is defined for natural numbers.
assert n > 0
# Base case.
if n == 1:
return [1]
f = []
# Check 2 first for saving half iterations in the next for loop.
while n % 2 == 0:
f.append(2)
n /= 2
# Check the odd numbers. We use `+ 1` because range does not include last
# value. It's equivalent to < instead of the <= that we want here.
for i in range(3, int(n**0.5) + 1, 2):
while n % i == 0:
f.append(i)
n /= i
# Prime number case.
if n > 1:
f.append(int(n))
return f
def eulers_phi_fun(n):
"""Euler's Totient function. """
f = prime_factors(n)
val = n
# Iterate for the unique list of primes.
for i in set(f):
val *= 1 - 1 / i
return int(val)
def solve(a, m):
"""Solve problem for the given a and m. """
gcd = math.gcd(a, m)
n = m / gcd
phi = eulers_phi_fun(n)
print(phi)
Referencias
Aquí te dejo una lista de enlaces que me ayudaron a entender de qué iba eso de la función \(\varphi\) de Euler. No solo explican qué es, sino que incluyen muy buenos ejemplos y demostraciones para entenderla en profundidad.
Altamente recomendados estos dos vídeos de Michael Penn:
- YouTube - Number Theory | Euler's Totient Function: Definition and Basic Example
- YouTube - The Multiplicativity of Euler's Totient Function
Otros recursos:
- Totient function en Wolfram Alpha
- Totient function en Wikipedia
- YouTube - Euler's Phi function proof
- Proof Wiki - Euler Phi Function is Multiplicative